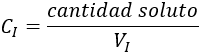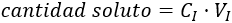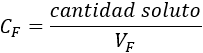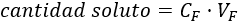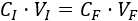Supongamos que disponemos de un volumen \(V_I\) (volumen inicial) de una disolución cuya concentración es \(C_I\) (concentración inicial).
Podemos definir \(C_I\) como la cantidad de soluto entre el volumen total de la disolución:
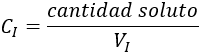
Despejando en esta fórmula, tenemos:
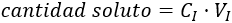
Al añadir disolvente a la disolución, el volumen de ésta cambia, por lo que lo denotamos por \(V_F\) (volumen final). Sin embargo, la cantidad de soluto es la misma, por lo que la concentración de la dilución (concentración final) es
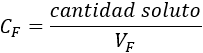
Despejando en esta fórmula, tenemos:
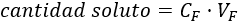
Como la cantidad de soluto es constante, podemos igualar ambas fórmulas obtenidas anteriormente:
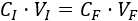
En los problemas veremos que la fórmula no sólo es aplicable para realizar una dilución añadiendo disolvente, sino también en otras situaciones como, por ejemplo, realizar una dilución (de volumen \(V_F\)) de una determinada concentración (\(C_F\)) tomando un volumen (\(V_I\)) de una disolución madre (de concentración \(C_I\)).
Notas:
-
Tanto las unidades empleadas para la concentración (porcentajes, molaridad…) como las empleadas para el volumen (mililitros, microlitros…) pueden ser distintas en cada situación, siempre que coincidan entre ellas.
-
Las soluciones de los problemas son extensas para facilitar su comprensión, pero, en realidad, sólo requieren un par de líneas.
-
Es imprescindible saber despejar la incógnita de la fórmula.
Problema 1
Se dispone de \(1\text{L}\) de una disolución de concentración \(0.7\text{M}\) de ácido cítrico en agua. ¿Cuánta agua debe añadirse para que obtener una dilución \(0.5\text{M}\)?
Ver solución
La concentración y el volumen iniciales son \(C_I = 0.7\text{M}\) y \(V_I = 1\text{L}\), respectivamente.
La concentración final debe ser \(C_F = 0.5\text{M}\).
Despejamos el volumen final en la fórmula:
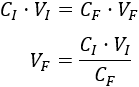
Sustituimos los datos:
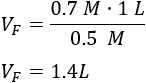
Como el volumen final debe ser \(1.4\text{L}\) y se parte de \(1\text{L}\), deben añadirse \(0.4\text{L}\) de agua.
Problema 2
Se dispone de una disolución de ácido clorhídrico en agua de concentración \(0.2\text{M}\). ¿Qué volumen de esta disolución debe tomarse para obtener una dilución de \(2\text{L}\) de concentración \(0.03\text{M}\)?
Ver solución
La concentración inicial es \(C_I = 0.2\text{M}\).
La concentración y el volumen finales son \(C_F = 0.03\text{M}\) y \(V_F = 2\text{L}\), respectivamente.
Despejamos el volumen inicial en la fórmula:
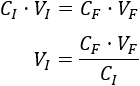
Sustituimos los datos:
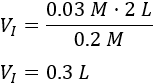
Se necesitan \(0.3\text{L}\) de la disolución inicial y \(1.7\text{L}\) de agua.
Problema 3
Se toman \(50 \text{ml}\) de una disolución de amoníaco en agua \(1 \text{M}\) y se añaden a un matraz que contiene \(30 \text{ml}\) de agua. ¿Cuál es la concentración de amoníaco de la dilución del matraz?
Ver solución
Tras añadir la disolución, el matraz contiene \(80 \text{ml}\). Esta cantidad es el volumen final: \(V_F = 80 \text{ml}\).
La concentración inicial es \(C_I = 1 \text{M}\).
El volumen inicial es el volumen que se traspasa: \(V_I = 50 \text{ml}\).
Despejamos en la fórmula la concentración final:
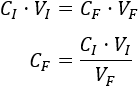
Sustituimos los datos:
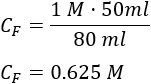
Por tanto, la concentración de la dilución obtenida es \(0.625 \text{M}\).
Problema 4
Se tienen \(50 \text{cl}\) una dilución de cloruro sódico en agua a una concentración de \(0.06 \text{M}\) que se ha obtenido al diluir en agua \(3 \text{cl}\) de una disolución madre. ¿Cuál es la concentración de cloruro sódico de la disolución madre?
Ver solución
La concentración final es \(C_F = 0.06 \text{M}\).
El volumen final es \(50 \text{cl}\).
El volumen inicial es \(V_I = 3 \text{cl}\).
Despejamos la concentración inicial en la fórmula:
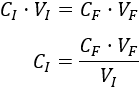
Sustituimos los datos:
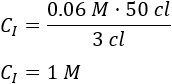
Por tanto, la concentración de la disolución madre es \(1 \text{M}\).
Problema 5
Calcular el volumen necesario de la solución madre de concentración \(36\%\) para preparar una dilución de \(102\text{ml}\) cuya concentración sea del \(6\%\).
Ver solución
La concentración inicial es \(C_I = 36\%\) y la final es \(C_F = 6\%\).
El volumen final es \(V_F = 102\text{ml}\).
Despejamos volumen inicial en la fórmula:
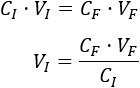
Sustituimos los datos:
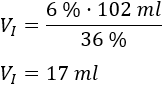
Por tanto, se requieren \(17\text{ml}\) de la solución madre.
Problema 6
De una disolución madre se toman \(10\text{ml}\) para preparar una dilución de concentración \(60\%\) que se usa, a su vez, para preparar \(100\text{ml}\) de una dilución de concentración \(3\%\). ¿Cuál es la concentración de la dilución madre?
Ver solución
-
Se realiza una primera dilución (dilución A) con concentración \(C^A = 60\% \).
-
Se realiza una segunda dilución (dilución B) con concentración \(C^B = 3\% \).
Observad que no podemos calcular la concentración de la disolución madre a partir de la primera dilución porque hay dos incógnitas en la fórmula: la concentración de la disolución madre y el volumen de la dilución A.
Podemos calcular el volumen de la dilución A, \(V_I\), que se ha utilizado para preparar la dilución B:
-
El volumen final es \(V_F = 100\text{ml}\).
-
La concentración final es \(C_F = C^B = 3\%\).
-
La concentración inicial es \(C_I = C^A = 60\%\).
Despejamos el volumen inicial:
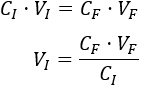
Sustituimos:
Se han utilizado \(V_I = 5 \text{ml}\) de la dilución A. Este volumen lo consideramos como el volumen total de la dilución A para usar el mínimo de producto.
Conociendo el volumen de la dilución A (volumen final), su concentración (concentración final) y el volumen de la disolución madre empleado (volumen inicial), podemos calcular la concentración de la disolución madre:
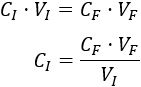
Sustituimos los datos:
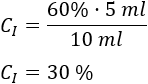
Por tanto, la concentración de la disolución madre es del \(30\%\).
Problema 7
Se quieren obtener dos diluciones a partir de \(5 \text{L}\) de ácido nítrico en agua con una concentración de \(0.4 \text{M}\).
-
Dilución A: \(30 \text{cl}\) y concentración de \(0.16 \text{M}\).
-
Dilución B: \(2.5 \text{dl}\) y concentración de \(0.2 \text{M}\).
¿Qué cantidades de la disolución madre y de agua se necesitan para realizar estas diluciones?
Ver solución
Lo primero a tener en cuenta es que debemos tener las mismas unidades para aplicar la fórmula. Pasamos a litros:
-
Dilución A: \(0.3 \text{L}\) y concentración de \(0.16 \text{M}\).
-
Dilución B: \(0.25 \text{L}\) y concentración de \(0.2 \text{M}\).
La concentración inicial es la misma en ambos casos: \(C_I = 0.4\text{M}\).
Dilución A:
La concentración y el volumen finales son \(C_F = 0.16 \text{M}\) y \(V_F =0.3 \text{L}\), respectivamente.
Despejamos en la fórmula el volumen inicial:
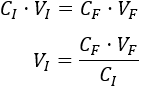
Sustituimos los datos:
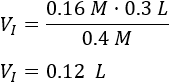
Se requieren \(0.12 \text{L}\) de la disolución madre. Calculamos la cantidad de agua necesaria:
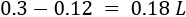
Dilución B:
La concentración y el volumen finales son \(C_F = 0.2 \text{M}\) y \(V_F =0.25 \text{L}\), respectivamente.
Despejamos en la fórmula el volumen inicial:
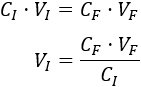
Sustituimos los datos:
Se requieren \(0.125 \text{L}\) de la disolución madre. Calculamos la cantidad de agua necesaria:
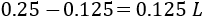
Recordamos que la concentración de una disolución es la relación que hay entre la cantidad de soluto y la cantidad de disolución; y diluir una disolución consiste en disminuir la proporción de soluto al aumentar la cantidad de disolvente. Por ejemplo, si disponemos de medio de vaso de agua salada, la concentración salina de esta disolución disminuye a la mitad si se llena el vaso con agua pura. 
